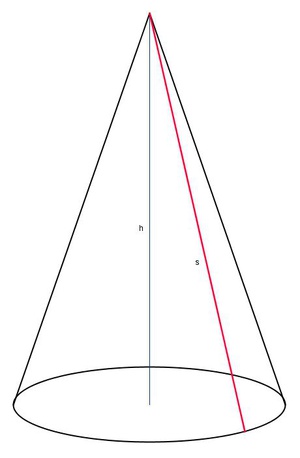
Die Mantellinie s eines Kegels
Als Mantellinie wird die kürzeste Verbindung zwischen einem beliebigen Punkt der Kreislinie der Grundfläche zur Spitze bezeichnet.
Die Mantellinie eines Zylinders wird mit s bezeichnet und liegt auf der Manteloberfläche.
Nachdem es unendlich viele Punkte auf der Kreislinie der Grundfläche gibt, gibt es auch unendlich viele Mantellinien.
Die Mantellinie s entspricht NICHT der Körperhöhe h des Zylinders.
Bei der Mantelfläche des Kegels handelt es sich um einen Kreisausschnitt. Der Radius dieses Kreisausschnittes entspricht dabei der Mantellinie s. Genaueres dazu finden Sie im Kapitel Das Netz eines Kegels .
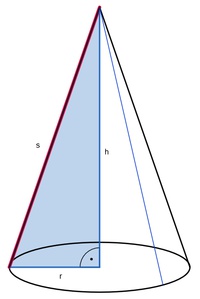
Die Länge der Mantellinie s berechnen.
Die Länge der Mantellinie s lässt sich mit Hilfe des "Lehrsatzes des Pythagoras berechnen" - vorausgesetzt, man kennt den Radius r oder Durchmesser d der Grundfläche sowie die Höhe h des Kegels.
Radius, Höhe und Mantellinie bilden ein rechtwinkeliges Dreieck. In jedem rechtwinkeligen Dreieck gilt der Lehrsatz des Pythagoras:
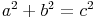
Die Summe der beiden Kathetenquadrate ist gleich dem Hypotenusenquadrat.
Die beiden Katheten (kürzeren Seiten) in unserem rechtwinkeligen Dreieck heißen r und h, die Hypotenuse (längste Seite; liegt dem rechten Winkel gegenüber) heißt s.
Somit können wir die oben genannte Formel an unsere Bedürfnisse anpassen und umformen:
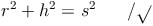
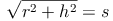
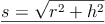
Als Mantellinie s wird die kürzeste Verbindung zwischen einem beliebigen Punkt der Kreislinie der Grundfläche zur Spitze bezeichnet.
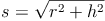
- Dieser Artikel hat mir geholfen. das half mir
- ... leider nicht ... leider nicht
- Kommentar Kommentar