Die Oberfläche des dreiseitigen Prismas
Ein dreiseitiges Prisma besteht aus der Grundfläche und der kongruenten Deckfläche sowie 3 unterschiedlichen Seitenflächen, die zusammen den Mantel bilden.
Die Oberfläche setzt sich nun aus diesen 5 Flächen zusammen. Die Grund- und Deckfläche sind kongruent, daher fassen wir sie als Grundfläche zusammen. Die 3 Seitenflächen fassen wir als Mantel zusammen:
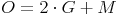
Grundfläche:
Bei einem dreiseitigen Prisma handelt es sich bei der Grundfläche um ein Dreieck. Da Grund- und Deckfläche kongruent sind, also um 2 gleich große Dreiecke.
Mantel:
Schneidet man das dreiseitige Prisma entlang einer senkrechten Kante auf und klappt die beiden Seitenflächen vor, so liegen nun 3 Rechtecke nebeneinander.
Sie bilden zusammen ein großes Rechteck. Die Breite dieser großen Rechtecks entspricht der Höhe des Prismas, die Länge entspricht der Summe der 3 Seitenlängen der Grundfläche (= Umfang der Grundfläche):
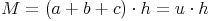
Grundfläche = Rechtwinkeliges Dreieck:
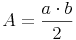
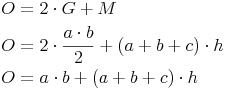
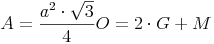
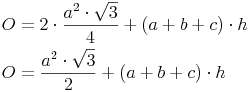
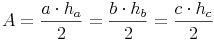
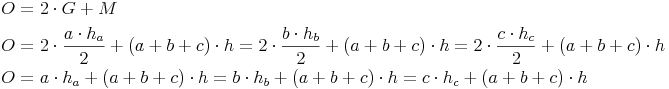
Oberfläche = 2 mal Grundfläche + Mantel
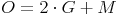
- Dieser Artikel hat mir geholfen. das half mir
- ... leider nicht ... leider nicht
- Kommentar Kommentar
julia
naja es geht
staf
wahr sehr hilfreich danke
Ansl
Naja nicht wirklich es könnte auch sein das ich einfach meinen Suchbegriff falsch eingegeben habe aber es war nicht das wonach ich suchte!
Dr. Hayan Hadba
Vielen herzlichen Dank