Die Seitenhöhe einer dreiseitigen Pyramide berechnen
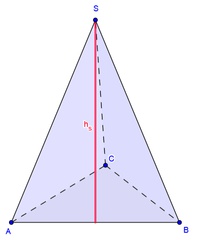
Die Seitenhöhe einer dreiseitigen Pyramide ist die Höhe einer der drei Seitenflächen (ABS, BCS, CAS).
Sie ist der kürzeste Abstand (= Normalabstand) einer Kante der Grundfläche (a, b, c) zur Spitze S.
Somit steht sie normal (= im rechten Winkel) auf eine Kante der Grundfläche und verläuft zur Spitze.
Bei einer gerade dreiseitigen Pyramide liegt die Spitze S genau oberhalb des Schwerpunktes der Grundfläche (siehe dazu Kapitel Körperhöhe). Daher handelt es sich bei den drei Seitenflächen um gleichschenklige Dreiecke.
Seitenhöhe vs. Körperhöhe:
Die Seitenhöhe ist nicht zu verwechseln mit der Körperhöhe!
Die Körperhöhe verbindet den Schwerpunkt der Grundfläche mit der Spitze und ist auf jedem Fall kürzer als die Seitenhöhe.
Berechnung der Länge der Seitenhöhe
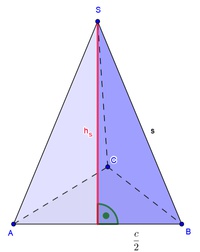
Zeichnet man die Höhe ein, so teilt diese das gleichschenklige Dreieck in zwei gleich große rechtwinkelige Dreiecke.
In einem rechtwinkeligen Dreieck gilt der Lehrsatz des Pythagoras, daher gilt:
Die Summe der beiden kürzeren Seiten (Katheten) jeweils hoch 2 ergibt die Hypotenuse hoch 2.
In unserem Beispiel heißen die beiden Katheten c/2und hs, die Hypotenuse s. Kurz:
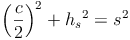
Wir formen um: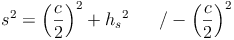
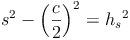
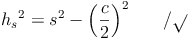
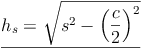
Geiches gilt natürlich auch für die beiden anderen Seitenhöhen: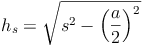
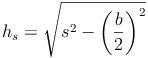
Die Seitenhöhe einer dreiseitigen Pyramide ist die Höhe einer der drei Seitenflächen (ABS, BCS, CAS).
Sie ist der kürzeste Abstand (= Normalabstand) einer Kante der Grundfläche (a, b, c) zur Spitze S, steht normal (= im rechten Winkel) auf eine Kante der Grundfläche und verläuft zur Spitze.
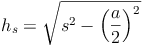 bzw.
bzw. 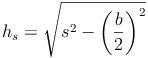 bzw.
bzw. 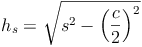
- Dieser Artikel hat mir geholfen. das half mir
- ... leider nicht ... leider nicht
- Kommentar Kommentar