Kardinalität / Mächtigkeit

M sei eine endliche Menge. Die Kardinalität (oder auch Mächtigkeit) von M ist die Anzahl der Elemente der Menge M.

Kardinalität/Mächtigkeit einer Menge

M sei eine endliche Menge. Die Kardinalität (oder auch Mächtigkeit) von M ist die Anzahl der Elemente der Menge M.

Beispiel 1:

A=\{0,1,2,3,4,5\}

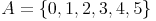
Die Menge A hat die Kardinalität 6:

|A|=6

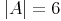
Beispiel 2:

B=\{19\}

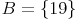
Die Menge B hat die Kardinalität 1:

|B|=1

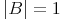
Beispiel 3:

C=\{0,1,2\}

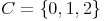
Die Menge C hat die Kardinalität 3:

|C|=3

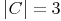
Kardinalität/Mächtigkeit einer Potenzmenge

Betrachtet man die Kardinalität einer Menge und die Kardinalität der dazugehörigen Potenzmenge, erkennt man einen Zusammenhang:

Menge mit 1 Element: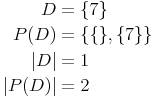

\begin{align} D & =\{7\} \\ P(D) & =\{\{\},\{7\}\} \\ |D| & =1 \\ |P(D)| & = 2 \\ \end{align}

Menge mit 2 Elemente: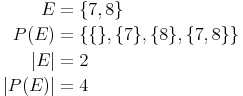

\begin{align} E & =\{7,8\} \\ P(E) & =\{\{\},\{7\},\{8\},\{7,8\}\} \\ |E| & =2 \\ |P(E)| & = 4 \\ \end{align}

Menge mit 3 Elemente: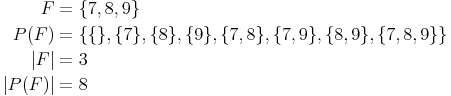

\begin{align} F & =\{7,8,9\} \\ P(F) & = \{\{\},\{7\},\{8\},\{9\},\{7,8\},\{7,9\},\{8,9\},\{7,8,9\}\} \\ |F| & = 3 \\ |P(F)| & = 8 \\ \end{align}

Man erkennt einen Zusammenhang zwischen der Mächtigkeit der Menge und der Mächtigkeit der Potenzmenge, und zwar:

|P(M)|=2^{|M|}

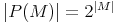
Erklärung:

Die Menge F hat 3 Elemente, daher hat die Potenzmenge P(F) 23=8 Elemente.

Kommentar #39474 von ric 17.04.17 10:43
ric

hallo, unglaublich, daß ich mit 46 Jahren nochmal in die Mengenlehre schauen muß. Die ersten Artikel sind sehr hilfreich, ich muß aber unbekannte Teilmengen in einer ganzen Menge finden(rechnerisch).Werde also weiterlesen.

Kommentar verfassen